Płyn doskonały i ciągłość strugi

Hydrostatykę mamy już za sobą, przejdźmy więc do hydrodynamiki. Dziś w menu zasada ciągłości strugi i omówienie założeń dla których jest ona prawdziwa.

Równanie ciągłości strugi

Równanie ciągłości strugi mówi nam o tym, że w objętość płynu wpływającego i wypływającego z dowolnego przekroju przewodu jest taka sama w jednostce czasu. Najłatwiej jest to zrozumieć wyobrażając sobie rurkę o dowolnym – może być o stałym, może być o zmienny – przekroju, do której dopływa pewna ilość wody i wypływa dokładnie tyle samo. Pamiętajcie, w przyrodzie nic nie ginie! Jednak to nie wszystko, musimy pamiętać, że powyższe rozważanie dotyczy płynu doskonałego.

Płyn doskonały

Czymże jest ten płyn doskonały? Jest to alkohol metylowy! Boże jaki żal, patrzcie jak foka płacze Jest to taki płyn, które jest nielepki, nieściśliwy, a przepływ jest stacjonarny i nie występują zawirowania.

• Nielepkość odnosi się do tarcia wewnętrznego powodowanego wzajemnym oddziaływaniem na siebie warstw (cząstek) płynu w czasie trwania przepływu, jednak nie dotyczy to oporu związanego z tarciem o ścianki naczynia. Jest co cecha związana z dynamiką płynu
• Nieściśliwość oznacza niezdolności do zmiany objętości pod wpływem sił zewnętrznych
• Przepływ stacjonarny (ustalony) zachodzi wówczas gdy prędkość, gęstość oraz ciśnienie w każdym punkcie są stałe i niezmienne w czasie
• Przy braku zawirowań wszystkie cząstki płynu poruszają się po torach równoległych do osi przewodu, co nazywamy także przepływem laminarnym lub warstwowym.

Linie prądu i struga

Należy wprowadzić jeszcze dwa pojęcia, a mianowicie linie prądu oraz strugę. Linie prądu są styczne do wektorów prędkości poruszających się cząstek, a struga jest skończoną wiązką tych linii. W przepływie stacjonarnym linie prądu pokrywają się z torami ruchu cząstek wody.

Przejdźmy do kolejnego etapu, w którym zmierzymy się z równaniem ciągłości strugi. Narysujmy fragment przewodu zamkniętego o zmiennej geometrii, z którego wydzielimy jedną strugę.

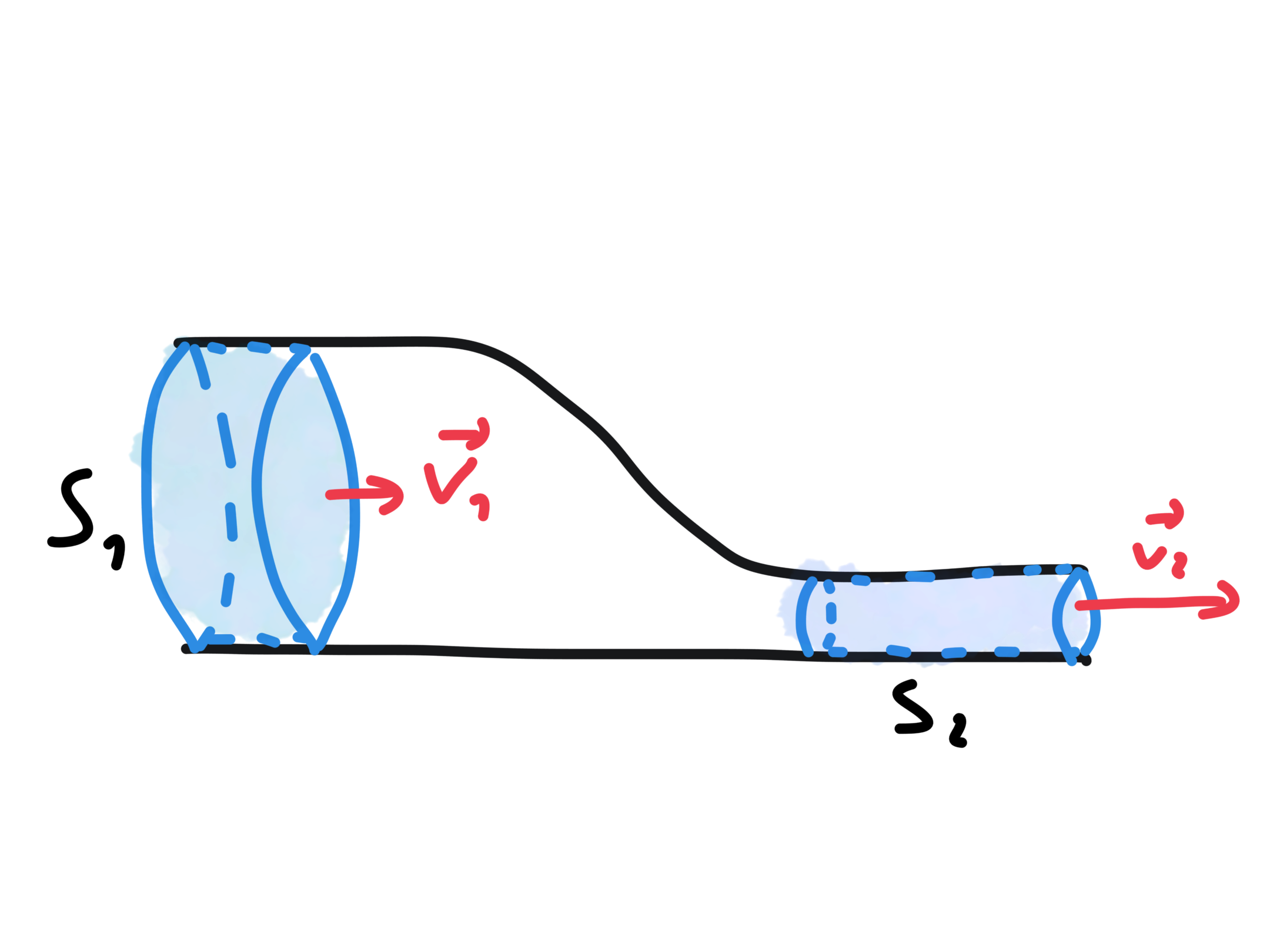
Wyprowadzenie równania

Jak widać, przekrój S_{1}, przez który wpływa nasz płyn ma większą powierzchnię niż przekrój zamykający S_{2}. Uważny obserwator dostrzeże również, że wektory prędkości v_{1} i v_{2} mają różne długości. Pamiętając o tym, że rozpatrujemy płyn idealny, wiemy że masa wpływająca jest równa masie wypływającej w jednostce czasu Zacznijmy jednak nie od masy, lecz od ciężaru właściwego naszego płynu i wyprowadzenia innych ważnych zależności. Czym jest ciężar właściwy? Jest to stosunek ciężaru do jego objętości:

γ = \frac{G}{V} [N\times m^{-3}]

Drugą ważną jednostką jest gęstość, czyli stosunek masy do objętości:

ρ = \frac{m}{V} [kg\times m^{-3}]

Masę możemy zapisać również jako stosunek ciężaru do przyspieszenia ziemskiego:

m = \frac{G}{g}

Dzięki poniższemu przekształceniu:

ρ = \frac{m}{V} = \frac{G}{gV} = \frac{γ}{g}

otrzymujemy poniższe zależności między gęstością i ciężarem właściwym płynu:

ρ = \frac{γ}{g}

γ = ρg

Z tą wiedzą możemy wrócić do równania ciągłości. Tak jak już wspomniano, masa płynu dopływającej jest równa masie płynu wypływającej, czyli:

Δm_{1} = Δm_{2}

zapiszmy to jednak w inny sposób:

Δm_{1} = ρΔV_{1} = ρS_{1}v_{1}Δt

Z definicji wiemy, że masa jest iloczynem gęstości i elementarnej objętości, czyli tym samy co gęstość pomnożona przez objętość walca, który jest wycinkiem strugi. Objętość walca zależna jest od pola podstawy, czyli pola powierzchni przekroju przewodu oraz wysokości, która w tym przypadku może być traktowana jako droga pokonana przez cząstkę płynu. Analogicznie możemy zapisać równanie dla przekroju zamykającego:

Δm_{2} = ρΔV_{2} = ρS_{2}v_{2}Δt

a po uproszczeniu:

S_{1}v_{1} = S_{2}v_{2}

Oznacza to, że wraz ze zmianą powierzchni przekroju, następuje zmiana prędkości. W naszym przypadku pole powierzchni przekroju maleje na długości, wiec prędkość wzrasta.

W tym miejscu odsyłam do kolejnego filmy PWr, w odcinku 58 został omówiony temat ciągłości strugi. Klik!